Question

A history professor decides to give a 10-question true-false quiz. She wants to choose the passing grade such that the probability of passing a student who guesses on every question is less than 0.10. What score should be set as the lowest passing grade?

Answer 1

Given data

10 question true-false

Procedure

This is a binomial probability problem. Where we have two outcomes which are pass or fail. We want the probability to be less than or equal to 10%.

We assume that the probability of passing the exam is 60% which corresponds to 6/10 correct questions.

Recall that the probability for the binonamial distribution is

`\text{NCn(p)}^np^(N-n)`

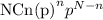
where:

N = Total problems

n = problems you have correct

p = probability of getting problem right

Calculating for a score of 60%

`\begin{gathered} P(X\ge x)=10C6(0.5)^6(0.5)^4 \\ P(X\ge x)=0.3769 \end{gathered}`

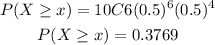
Now, Let's try with a higher grade value to pass (80%)

`\begin{gathered} P(X\ge x)=10C8(0.5)^8\cdot0.5^2 \\ P(X\ge x)=0.0546875 \end{gathered}`

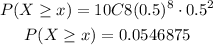
The passing grade would be 80%, i.e. getting 8 correct questions.