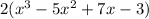Question

Write a polynomial function in factored form that has degree 3 with x intercepts at x = 1 and x = 3 with even multiplicity at x = 1 and y intercept at -6

Answer 1

`2(x^3-5x^2+7x-3)=2x^3-10x^2+14x-6`

Step-by-step explanation:

Here, we want to get the polynomial function

We expect 3 roots

This means there should be 3 x-intercepts

One of the intercepts has an even multiplicity, that means it occurred twice 9since our maximum occurrence is 3)

The general form of the degree 3 polynomial is:

`f(x)=ax^3+bx^2\text{ + cx + d}`

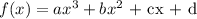
where d is the y-intercept. This is the value of f(x) when x is zero

Let us take a look at the x-intercepts:

We have them as:

(x-1)(x-1)(x-3)

Opening up these brackets, we have:

`\begin{gathered} (x-1)(x-1)(x-3)\text{ = } \\ (x-3)(x^2-2x\text{ + 1)} \\ =x^3-2x^2+x-3x^2\text{ + 6x - 3} \\ =x^3-5x^2+7x-3 \end{gathered}`

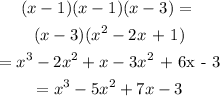
Recall, the y-intercept is -6

We have to multiply the whole expression by 2 as follows:

`2(x^3-5x^2+7x-3)`