Given two parallel lines intersected by a transversal, you can identify the following pair of angles:

Notice that those angles are located on the same side of the transversal. One of them is exterior and the other angle is exterior. Therefore, they are a special pair of angles called "Corresponding Angles".
By definition, Corresponding Angles are congruent, which means that they have equal measure.
Knowing that you can set up the following equation:
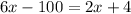
Now you can solve for "x" in order to find its value:
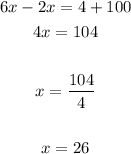
Now you can substitute the value of "x" into one of the expressio