Question

Points W and X are on Wx. Y and Z are on YZ. Are WX and YZ parallel, perpendicular, Or neither?3.) W(2, 1) X(6, 2) Y(2, "-2)" Z(6, "-2)"

Answer 1

Neither parallel nor perpendicular

Step-by-step explanation

To find if the lines are parallel or perpendicular, we have to find the slopes.

The slope of a line passing through points (x₁, y₁) and (x₂, y₂) is,

`m=(y_1-y_2)/(x_1-x_2)`

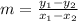
The slope of line WX, passing through points W(2, 1) and X(6, 2) is,

`m_(WX)=(1-2)/(2-6)=(-1)/(-4)=(1)/(4)`

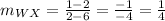
The slope of line YZ, passing through points Y(2, -2) and Z(6, -2) is,

`m_(YZ)=(-2-(-2))/(2-6)=(-2+2)/(-4)=0`

Two lines are parallel if they have the same slope, and perpendicular if they have opposite reciprocal slopes.

In this case, the slopes are 1/4 and 0, which are neither the same nor opposite reciprocals.

Hence, lines WX and YZ are neither parallel nor perpendicular.