Question

complete the table below: country a.Growth rate: 1.1% per year Doubling time: _________country b. Growth rate: ___ per year. Doubling time: 36 years

Answer 1

country a.

Growth rate: 1.1% per year

Doubling time: 63 years



country b.

Growth rate: 1.9% per year.

Doubling time: 36 years​

Step-by-step explanation:

Given that the population is doubled, the growth rate for country a is 1.1% per year, the doubling time is given by the formula:

`T_d=(\ln (2))/(\ln (1+k))`

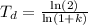
Where k is the growth rate

`\begin{gathered} T_d=(\ln (2))/(\ln (1+(1.1)/(100))) \\ \\ =(\ln (2))/(\ln (1.011)) \\ \\ =63 \end{gathered}`

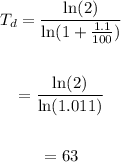
The Doubling time is 63 years

For a doubling time of 36 years, we want to find the growth rate.

`\begin{gathered} 36=(\ln (2))/(\ln (1+k)) \\ \\ \ln (1+k)=(\ln (2))/(36) \\ \\ \text{Taking the exponential of both sides} \\ 1+k=e^{(\ln (2))/(36)} \\ \\ k=e^{(\ln(2))/(36)}-1 \\ \\ =0.019 \end{gathered}`

This is 1.9%, and it is the growth rate.