Given,
The principal amount is $16000.
The time period is 5 years.
a)The rate of interest is 5%.
The amount compounded quarterly is,
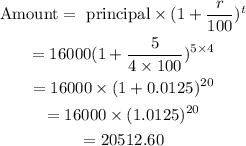
Hence, the amount compounded quarterly is $20512.60.
b)The rate of interest is 5%.
The amount compounded monthly is,

Hence, the amount compounded monthy is $20533.74.
c)The rate of interest is 3%.
The amount compounded quarterly is,

Hence, the amount compounded quarterly is $18578.95.
d)The rate of interest is 3%.
The amount compounded monthly is,
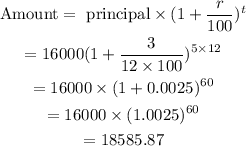
Hence, the amount compounded monthy is $18,585.87.