Question

samir opened a savings account 7 years ago the account earns 11% interest compounded monthly if the current balance is 500.00 how much did he deposit initially

Answer 1

We know that

• The period of time is 7 years.

,

• The interest is 11% compounded monthly.

,

• The current balance is 500.

We have to use the compound interest formula

`A=P(1+(r)/(n))^(nt)`

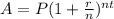
Replacing the given information, we have.

`500=P(1+(0.11)/(12))^(12(7))`

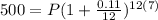
Then, we solve for P.

`\begin{gathered} 500=P(1+0.0092)^(84) \\ 500=P(1.0092)^(84) \\ 500=P(2.16) \\ P=(500)/(2.16) \\ P\approx231.48 \end{gathered}`

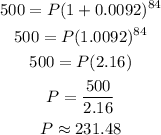
Hence, the initial deposit was $231.48, approximately.