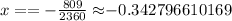Question

(6x+2.4):3 /59=2.25:1/3 find x

Answer 1

We will interpret the question as follows:

`(6x+2.4)\colon(3)/(59)=2.25\colon(1)/(3)`

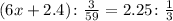
The symbol, :, denotes the ratio of two quantities. Then, we can rewrite it as follows:

`((6x+2.4))/((3)/(59))=(2.25)/((1)/(3))`

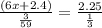
Using proportions, we can multiply the means of the proportions by the extremes of them as follows:

`(1)/(3)(6x+2.4)=2.25\cdot(3)/(59)`

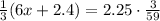
We have that:

`2.25=2+(1)/(4)=(8+1)/(4)=(9)/(4)`

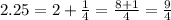
And

`2.4=(24)/(10)=(12)/(5)`

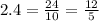
Then, we have:

`(1)/(3)(6x+2.4)=2.25\cdot(3)/(59)\Rightarrow(1)/(3)(6x+(12)/(5))=(9)/(4)(3)/(59)`

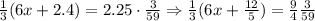
We can multiply by 3 to both sides of the equation:

`3\cdot(1)/(3)(6x+(12)/(5))=3(9)/(4)(3)/(59)`
`6x+(12)/(5)=(9)/(4)(9)/(59)`

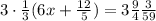
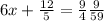
Subtracting 12/5 from both sides of the equation:

`6x+(12)/(5)-(12)/(5)=(9)/(4)(9)/(59)-(12)/(5)`
`6x=(9)/(4)(9)/(59)-(12)/(5)`

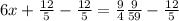
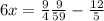
If we multiply both sides by 1/6, we finally have:

`(1)/(6)6x=(1)/(6)((9)/(4)(9)/(59)-(12)/(5))`
`x=(1)/(6)((9)/(4)(9)/(59)-(12)/(5))=-(809)/(2360)\approx$$-0.342796610169$$`

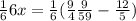
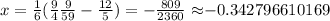
In summary, the value for x in fractional and also in decimal form is:

`x==-(809)/(2360)\approx$$-0.342796610169$$`