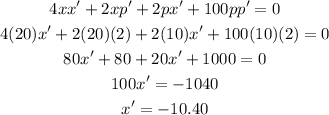A price p (in dollars) and demand x (in items) for a product are related by
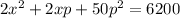
If price is increasing at a rate of $2 per month. Therefore,
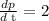
Now, from the given equation using p=10,
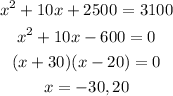
Since, demand can't be negative, therefore,
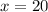
Now, differentiating the given equation w.r.t t and then putting x=20,p=-10,