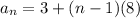The sequence we have is:
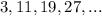
To find the arithmetic sequence, we use the arithmetic sequence formula:
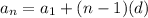
Where
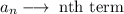
Note: n can be any number
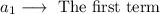
Since the first term, in this case, is 3:
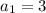
And d is the common difference between the terms.
As we can see in the following image, the common difference is +8:
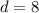
So the rule for the arithmetic sequence for a term "n" is:
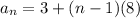
Answer: