Question

How many more adults than students bought tickets to the concert?

Answer 1

Let's use the letter A to represent the number of adult tickets, and S to represent the number of student tickets.

We know that the total number of sold tickets was 175 (assuming everyone who bought a ticket went to the concert).

Thus, we can write:

`A+S=175`

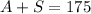
We also know that the number of sold adult tickets was 10 more than twice the number of student tickets. Thus, we have:

`A=10+2S`

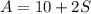
Now, notice that the first equation can be written as:

`S=175-A`

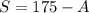
Then, using the above result into the second equation, we obtain:

`\begin{gathered} A=10+2(175-A) \\ \\ A=10+350-2A \\ \\ A+2A=360-2A+2A \\ \\ 3A=360 \\ \\ (3A)/(3)=(360)/(3) \\ \\ A=120 \end{gathered}`

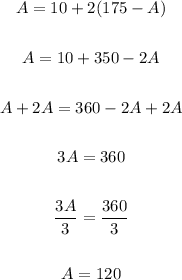
Now, we can use the previous result to find S:

`S=175-120=55`

Since we need to find how many more adults than students bought tickets, we need to subtract 55 from 120:

`120-55=65`

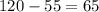
Therefore, the answer is 65.