Question

11. A bag contains 6 white counters, 7 black counters, and 4 green counters. What is the probability of drawing(a) a white counter or a green counter? (b) a black counter or a green counter? (c) not a green counter?

Answer 1

We know that the bag contains:

• 6 white counters,

,

• 7 black counters,

,

• 4 green counters,

,

• 17 counters in total.

We define the events:

• W = draw a white counter,

,

• B = draw a black counter,

,

• G = draw a green counter.

,

•

We have the following probabilities:

• P(W) = # white counters / total # of counters = 6/17,

,

• P(B) = # black counters / total # of counters = 7/17,

,

• P(G) = # green counters / total # of counters = 4/17,

(a) First, we compute:

P(W and G) = # white and green counters / total # of counters = 0/17 = 0.

The probability of drawing a white counter or a green counter is given by:

`P(\text{W or }G)=P(W)+P(G)-P(W\text{ and G)}=(6)/(17)+(4)/(17)=(10)/(17)`

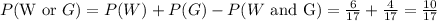
(b) First, we compute:

P(B and G) = # black and green counters / total # of counters = 0/17 = 0.

The probability of drawing a black counter or a green counter is given by::

`P(B\text{ or }G)=P(B)+P(G)-P(B\text{ and G)}=(7)/(17)+(4)/(17)=(11)/(17)`

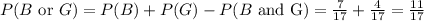
(c) The probability of not drawing a green counter is:

`P(\text{not G)}=1-P(G)=1-(4)/(17)=(17-4)/(17)=(13)/(17)`

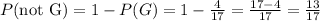
Answers

• (a) P(W or G) = 10/17

,

• (b) P(B or G) = 11/17

,

• (c) P(not G) = 13/17