Let us divide the composite figure into two shapes: parallelogram and trapezoid. The sum of the area of both shapes will give the total area of the composite shape.
Area of the parallelogram:
The area of a parallelogram, A₁, is given by
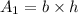
The area is thus calculated as
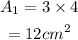
The area of the parallelogram is equal to 12 cm²
Area of the trapezoid:
The area of a trapezoid, A₂, is given by
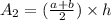
The area is thus calculated as

The area of the trapezoid is equal to 12 cm²
Total Area of Composite Figure
The total area, A, is given as
![\begin{gathered} A=A_1+A_2 \\ =12+12 \\ A=24\operatorname{cm} \end{gathered}]()
The area of the shape is 24 cm².
The correct option is OPTION C.