Given:
Two to the three-fourths power, all over two to the one half power
Find-:
Write the expression
Explanation-:
Applying the quotient rule for powers, which tells you that whenever you are dividing two powers, that have the same base and different power, you can copy the base and subtract the powers:
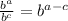
So,
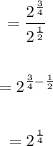
Radical expression using the formuli s:
![b^{(1)/(a)}=\sqrt[a]{b}](https://img.qammunity.org/2023/formulas/mathematics/college/atyloqs8du9vm7fo3cr4c76wajdcffrz5x.png)
So, the value is:
![2^{(1)/(4)}=\sqrt[4]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/wr8c8yl3b45g1jv7teopnk0n36nm48p0in.png)