ANSWER :
The rate of current is 3 miles/hour
EXPLANATION :
Let x be the rate of the boat
and
y be the rate of the current
The total rate downstream is x + y, since the current is adding a speed to their boat.
The total rate upstream is x - y, since the current is opposite to the direction of the boat.
Note that distance = rate x time
Their trip downstream is 2 hours while in upstream is 8 hours
Since the distance downstream and upstream is the same, we can express it by :
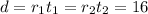
Where r1 is the downstream rate with t1 as the time.
r2 is the upstream rate with t2 as the time to go back
r1 = x + y
r2 = x - y
Substitute the values to the formula :
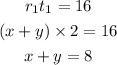
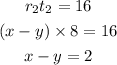
Now we have two equations,
Eq 1 : x + y = 8
Eq 2 : x - y = 2
Express Eq 1 as x in terms of y :
x + y = 8
x = 8 - y
Substitute this to Eq 2 :
x - y = 2
(8 - y) - y = 2
8 - 2y = 2
-2y = 2 - 8
-2y = -6
2y = 6
y = 6/2
y = 3