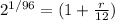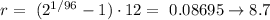For this problem we can use the future value formula given by:

Where P= 4000 represent the initial amount
A= 8000 represent the amount doubled
t= 8 represent the number of years
n= 12 assuming that the interest is compounded each year
r= represent the rate of interest that we want to find
So then we need to solve for r
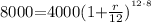
If we divide both sides by 4000 we got:
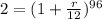
We apply exponentiation on both sides and we got: