Question

Question 1 Essay Worth 10 points)(07.03 MC)Complete the square to rewrite the following equation. Identify the center and radius of the circle. You must show all work and calculations to receive creditx2 - 4x + y + y = -4x

Answer 1

the solution is

`(x^{}-2)^2+(y+4)^2=16`

the center is in (x,y)=(2,4)

the radius is 4

to solve this, first we agroup the x's and y's,

`(x^2-4x)+(y^2+8y)=-4`

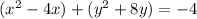
normaly, we would need to divide the whole equation by the coeficient of the squares

in this case the coeficient is 1 so we don't need to do that

now, we need to look at the coeficient of the x and y (not squared)

for x is -4 and for y is +8

we divide them bi two, and square them

-4/2=-2 => -2^2=4

8/2=4 => 4^2=16

and now we add this terms in the parentheses and add the to the right side of the equation

`(x^2-4x+4)+(y^2+8y+16)=-4+4+16`

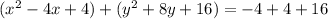
now, we need to simplify the parentheses and let them expresed as binomial squares

`(x-2)^2+(y+4)^2=16`

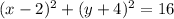
and thats the equation. now the term inside the parentheses that aren't x or y, tell us the center.

center (x,y)=(2,-4)

and the radius is the square root of the term in the right side

`\text{radius: }\sqrt[]{16}=4`