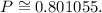Using the data of the table, we must find the probability that a randomly selected U.S. worker was not in either Wholesale Trade or Education & Health Services.
Let's define the following events:
• A = an employee works at Wholesale Trade,
,
• B = an employee works at Education & Health Services.
Now, the probability that an employee works in a particular area, it is equal to the quotient between the number of employees in that area and the total number of employees.
Using the data of the table we find that:
• P(A) = # employees at Wholesale Trade / total # of employees = 5,803.7/137,147.0 ≅ 0.04231226.
,
• P(B) = # employees at Education & Health Services / total # of employees = 21,481.0/137,147.0 ≅ 0.15662756.
Now, the probability that an employee is not in either Wholesale Trade or Education & Health Services, is given by:
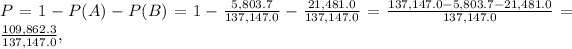
or to the nearest millonth:
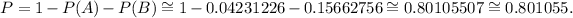
Answer
The probability that a randomly selected U.S. worker was not in either Wholesale Trade or Education & Health Services is:
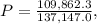
or to the nearest millonth: