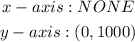Question

CIce1.) Caleb wants to invest $1000 in a savings account. Lincoln Fecompounded yearly. Washington National Bank is offeringa. For each bank, write an exponential function to represerin the account after t years.b. Determine which bank Caleb should choose if he plans tdecides to leave the money in the bank for a longer perideal in the long run? Explain your reasoning.c. Discuss the domain, range, asymptotes, intercepts, enddecrease for each function as they relate to this probler2. In 2010, Bolivia had a population of 10.5 million people and

Answer 1

initial investment, P = $1000

Linconln Federal Bank- LFB interest rate, 6% compounded yearly

Whashington National Bank- WNB interest rate, 5.5% compounded daily

a. exponential function

We'll use the compound interest formula

`A=P(1+(r)/(n))^(nt)`

where,

A=final amount

P=initial principal balance

r=interest rate

n=number of times interest applied per time period

t=number of time periods elapsed

we know that

P = $1000

t is in years

LFB, r = 0.06 compounded yearly , then n = 1

`\begin{gathered} A_(LFB)=1000(1+0.06)^t \\ A_(LFB)=1000*1.06^t \end{gathered}`

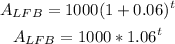
WNB, r = 0.05 compounded daily

`A_(WNB)=1000(1+(0.055)/(365))^(365*t)`

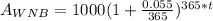
b

Let' see, if t = 10 years, then A-LFB = $1790.85 and A-WNB = $1733.18

Caleb should choose LFB

c.

the domain of these exponential functions is

`D:(-\infty,\infty)`

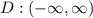
the range is,

`R:(0,\infty)`

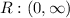
This functions have a horizontal asymptote at y = 0

behavior, since the base of the exponent is >1 this is an increasing function

intercepts,

`\begin{gathered} x-axis:NONE \\ y-axis:(0,1000) \end{gathered}`