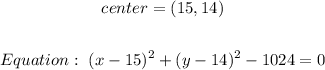The Solution:
Given the ends of a diameter:
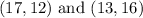
Required:
To write the equation of the circle.
Step 1:
Find the center of the circle by using the midpoint formula.
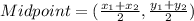
In this case,
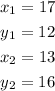
Substituting, we get
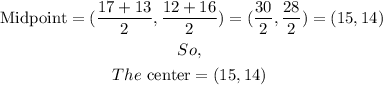
Step 2:
Find the radius of the circle.
Using the distance between two points formula:
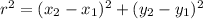
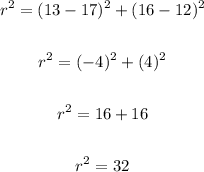
Step 3:
Write the equation of the circle.
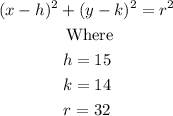
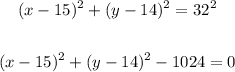
Therefore, the correct answers are: