1 Answer

Haresh Ambaliya · Answer 1 · 2023-02-07T16:50:43+0000

To find the total surface area of the box, we have to find the area of each part.

Area of the two equal triangles.

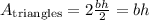
$A_{\text{triangles}}=2(bh)/(2)=bh$

Where b = 7m and h =8m.

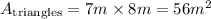
$A_{\text{triangles}}=7m*8m=56m^2$

Now, let's find the area of each rectangle because they are different,

$\begin{gathered} A_1=bh=13m\cdot7m=119m^2 \\ A_2=bh=13m\cdot8m=104m^2 \\ A_3=bh=13m\cdot10.63m=138.19m^2 \end{gathered}$

Then, we add all the areas

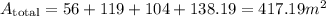
$A_{\text{total}}=56+119+104+138.19=417.19m^2$

Please log in or register to add a comment.