Question

The domain of y = ax^2 + c is all real numbers. Describe the range when (a) a > 0) and (b) a < 0. a. range when a > 0 b. range when a < 0

Answer 1

Range of a function

We know that the range of a function corresponds to the y-values it takes. For the function:

`y=ax^2+c`

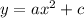
we want to find the y values it cannot take.

Step 1

Solving the equation for x.

We want to rearrange the equation:

`\begin{gathered} y=ax^2+c \\ \downarrow\text{substracting c both sides} \\ y-c=ax^2 \\ \downarrow\text{ dividing by a both sides} \\ (y-c)/(a)=x^2 \\ \downarrow\text{ square root of both sides} \\ \sqrt{(y-c)/(a)}=x \end{gathered}`

We know that in the real numbers, the square root of a negative number doesn't exist. Then

`\begin{gathered} \sqrt[]{(y-c)/(a)}=x \\ \downarrow \\ (y-c)/(a)\text{ cannot be negative} \\ \downarrow(y-c)/(a)\text{ is positive or 0} \\ (y-c)/(a)\ge0 \end{gathered}`

Step 2

Finding the range

When a > 0

Then

`\begin{gathered} (y-c)/(a)is\text{ positive if and only if } \\ y-c\ge0 \end{gathered}`

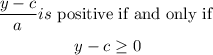
Adding c both sides:

`\begin{gathered} y-c\ge0 \\ y\ge c \end{gathered}`

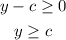
Then, y goes from c to infinity

`y\in\lbrack c,\infty)`

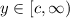
Answer A - Range = [c, ∞) when a >0

When a < 0

Then

`\begin{gathered} (y-c)/(a)is\text{ positive if and only if } \\ y-c\leq0 \end{gathered}`

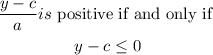
Because the division of two negative numbers is always positive

Adding c both sides:

`\begin{gathered} y-c\leq0 \\ y\leq c \end{gathered}`

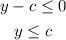
Then, y goes from minus infinity to c

`y\in(-\infty,c\rbrack`

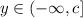
Answer - Range = (- ∞, c] when a < 0