Question

A 1900-pound car is parked on a street that makes an angle of 10° with the horizontal. Find the magnitude of the force required to keep the car from rolling down the hill.

Answer 1

329.93 Pounds

Step-by-step explanation

Step 1

Diagram andFre body diagram

and Free body diagram

Step 2

Newtons first law states that If a body has a net force acting on it, it is accelerated in accordance with the equation. Conversely, if a body is not accelerated, there is no net force acting on it.

so, as the car is at rest ( acceleration=0) the sum of the forces acting on it must equal zero,hence

for the x -axis

`\begin{gathered} ff-wsin\theta=0 \\ replace \\ ff-1900\text{ pound*sin10=0} \\ ff=329.93\text{ pounds} \end{gathered}`

so, the force of friction must be 329.93 Pounds

Step 3

force in newtons

to convert from pounds to Newtons we need to multiply by 4.44822

so

`\begin{gathered} 329.93\text{ Pound0}\Rightarrow329.93*4.44822\text{ N} \\ 329.93\text{ Pound0}\Rightarrow1140.91 \\ 329.93\text{ Pound0}\Rightarrow1141\text{ Newtons} \end{gathered}`

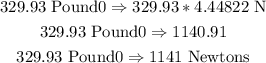
therefore, the answer is

1141 Newtons

I hope this helps you