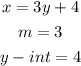Given:
Given that a graph of
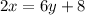
And
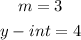
Required:
To find the error in the given statement.
Step-by-step explanation:
Slope-intercept form is
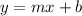
where m is the slope and b is the y-intercept.
Consider the given equation
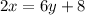
Here the slope intercept form is,
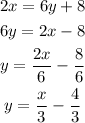
Now the slope is,
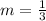
And y-intercept is,
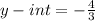
The correct graph is,
Final Answer:
The error is,
Intercept form: