Question

Two speakers that are 15.0 mproduce in-phase sound waves of frequency 250.Hz in a roomwhere the speed of sound is 340. m/s. A woman starts out at the midpoint between the two speakers.a.What does she hear at the midpoint, constructive or destructive interference?b.She now walks slowly towards one of the speakers. How far from the center must she walk before she first hears the sound reach a minimum intensity?c.How far from the center must she walk before she first hears the sound at a maximum intensity?d.How far from the center must she walk before the second time she hears the sound at the minimum intensity?

Answer 1

a. Constructive interference.

b.
`0.34\; \rm m`.

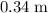c.
`0.68\; \rm m`.

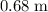d.
`1.02\; \rm m`.

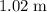Step-by-step explanation:

Frequency of this sound wave:
`f = 250\; \rm Hz = 250\; \rm s^(-1)`.

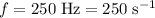Speed of this sound wave:
`v = 340\; \rm m \cdot s^(-1)`.

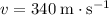Calculate the wavelength of this sound wave:

`\begin{aligned} \lambda &= (v)/(f) \\ &= \fraac{340\; \rm m \cdot s^(-1)}{250\; \rms^(-1)} \approx 1.36\; \rm m\end{aligned}`.

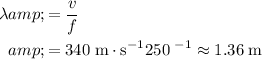Path difference refers to the absolute value of the difference between:

• the distance between the first source (the first speaker) and the observer, and
• the distance between the second source (the second speaker) and the observer.

When the observer in this question is on the line between the two speakers at
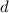`d` meters from the midpoint, the corresponding path difference would be
`2\; d` meters. (Add
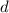`d\!` to the distance from the closer source, and subtract
`d\!\!` from the distance from the other source.)

The question states that sound from the two speakers are in-phase. In other words, at every instant, the sound wave from the two speakers are at the same phase at the position of each speaker.

Because wave from the two sources are in-phase at the source:

• Constructive interference happens when the path difference is an integer multiple of wavelength (
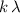  `k\, \lambda`, where
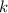  `k` is an integer.) That includes:
  `0`,
  `\lambda`,
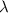  `2\, \lambda`, etc.
• Destructive interference happens when the path difference is an one-half plus some integer multiple of wavelength (
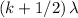  `(k + 1/2) \, \lambda`, where
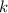  `k` is an integer.) That includes:
  `\lambda / 2`,
  `3\, \lambda / 2`,
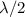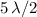  `5\, \lambda / 2`, etc.

Path difference is
`0` when the observer is at the midpoint. That would correspond to constructive interference.

The first destructive interference (minimum intensity) corresponds to a path difference of
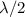`\lambda / 2`. Along the line, that would be observed at
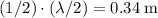`(1/2) \cdot (\lambda / 2) = 0.34\; \rm m` from the midpoint.

The next constructive interference (maximum intensity) would be observed when path difference is
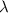`\lambda`. Along the line, that would be observed at
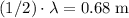`(1/2)\cdot \lambda = 0.68\; \rm m` from the midpoint.

The second destructive interference (minimum intensity) would be observed when path difference is
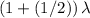`(1 + (1/2))\, \lambda`. Along the line, that would be observed at
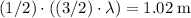`(1/2) \cdot ((3/2)\cdot \lambda) = 1.02\; \rm m` from the midpoint.