1 Answer

Maxsap · Answer 1 · 2023-11-16T10:48:03+0000

We need to solve the next expression using the properties of the logarithm:

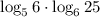
$\log _56\cdot\log _625$

Use the next logarithm property on both:

$\log _ab\text{ =}(\ln b)/(\ln a)$

So:

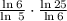
$\frac{\ln6}{\ln\text{ 5}}\cdot(\ln 25)/(\ln 6)$

Cancel the like terms, in this case, ln 6

Then:

$\frac{\ln \text{ 25}}{\ln 5}$

Rewrite the expression ln 25, using the next property:

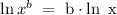
$\ln x^{b\text{ }}=\text{ b}\cdot\ln \text{ x}$

Then

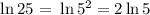
$\ln 25\text{ = }\ln 5^2=2\ln 5$

Simplify the like terms:

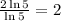
$(2\ln 5)/(\ln 5)=2$

Therefore, The result is 2.

Please log in or register to add a comment.