Question

Find a formula for the exponential function passing through the points (-1,1/2) and (1,8)

Answer 1

The general form of an exponential function is:

`f(x)=ab^x`

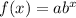
We are given the points:

`(-1,(1)/(2))\text{ }and\text{ }(1,8)`

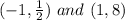
This means:

`\begin{gathered} f(-1)=(1)/(2) \\ . \\ f(1)=8 \end{gathered}`

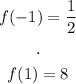
Thus, we can write:

`\begin{cases}(1)/(2)=ab^(-1){} \\ 8=ab^1\end{cases}`

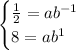
This is a system of two equations with two variables. We can solve for b in the first equation:

`\begin{gathered} (1)/(2)=ab^(-1) \\ . \\ (1)/(2)=(a)/(b) \\ . \\ b=2a \end{gathered}`

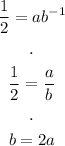
And now, substitute in the second equation:

`\begin{gathered} 8=a(2a)^1 \\ . \\ 8=2a^2 \\ . \\ (8)/(2)=a^2 \\ . \\ a=\pm√(4) \\ . \\ a=\pm2 \end{gathered}`

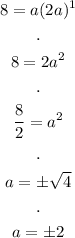
Now, we can pick any of the two solutions for a, in this case, we'll use the positive one, a = 2. And now we can find b:

`\begin{gathered} b=2\cdot2 \\ . \\ b=4 \end{gathered}`

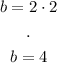
Now, we can write the equation:

`f(x)=2\cdot4^x`

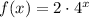
And we can verify that the points given lie in the graph of f(x), by evaluating:

`\begin{gathered} f(-1)=2\cdot4^(-1)=(2)/(4)=(1)/(2) \\ . \\ f(1)=2\cdot4^1=2\cdot4=8 \end{gathered}`

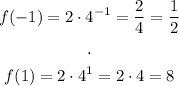
Thus, the answer:

`f(x)=2\cdot4^x`

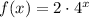
is correct.