1) Albert
To determine the balance of Albert's $2000 after 10 years you have to calculate the ending balance of each investment he did and then add them together.
a) $1000 earned 1.2% annual interest compounded monthly.
To determine the final balance after 10 years you have to apply the following formula:
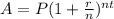
Where
A is the accrued amount (initial + interest)
P is the principal/ initial amount
r is the interest rate, expressed as a decimal value
n is the number of compounding periods per year
t is the number of years
For this investment:
P= $1000
r=0.012
n= 12 → the interest is compounded monthly, there are 12 months in a year, so there are 12 compound periods per year.
t=10 years
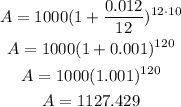
After 10 years, the final balance for this investment will be $1127.43
b) $500 lost 2% over the course of the 10 years
This investment lost 2% over the 10 years, to determine how much was lost you have to calculate the 2% of 500:
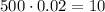
Then subtract the calculated amount from the initial investment to determine the final balance:
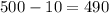
After 10 years, the final balance for this investment will be $490
c) $500 grew compounded continuously at a rate of 0.8% annually
To calculate the accrued amount for an account that compounds continuously you have to apply the following formula:
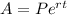
Where
A is the accrued amount
P is the principal amount
r is the interest rate expressed as a decimal value
t is the time in years
e is the natural number
For this investment:
P=$500
r=0.8/100=0.008
t=10
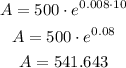
After 10 years the final balance will be $541.64
d) Add the three results to determine the total balance of Albert's $2000 after the 10 years:
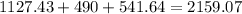
Albert's balance after 10 years will be $2159.07
2) Marie
a) $1500 earned 1.4% annual interest compounded quarterly
To determine the final balance of this investment after 10 years you have to use the same formula as in the first part of the previous question:
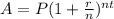
For this investment:
P= $1500
r= 1.4/100=0.014
n=4 → the account compounds quarterly, which means once every 3 months, there are 4 quarters per month.
t=10 years
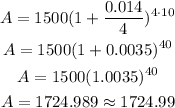
The final balance for this investment is $1724.99
b) $500 gained 4% over the course of 10 years.
To determine how much was won over the 10 year period you have to calculate the 4% of 500
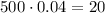
Add this amount to the initial investment to determine the final balance:
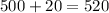
The final balance for this investment is $520
c) Add both results to determine the final balance of the investment after 10 years:
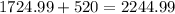
Marie's balance after 10 years will be $2244.99
3) Hans
$2000 grew compounded continuously at a rate of 0.9% annually.
The account compounds continuously, so to calculate the final balance you have to use the formula:
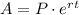
For this investment
P= $2000
r=0.9/100=0.009
t=10
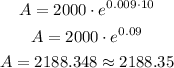
Hans's balance after 10 years will be $2188.35.
4) Max
a) $1000 decreased in value exponentially at a rate of 0.5% annually
To determine the final balance of this investment you can determine an exponential decrease:
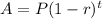
A corresponds to the accrued amount
P is the principal amount
r is the decrease rate, expressed as a decimal value
t is the time in years
For this investment
P=$1000
r=0.5/100=0.005
t=10 years
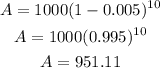
The balance after 10 years will be $951.11
b) $1000 earned 1.8% annual interest compounded biannually
For this part, use the formula:
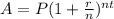
For this investment
P=$1000
r=1.8/100=0.018
n=2 → the account compounds annually, there are two compounding periods per year.
t=10 years
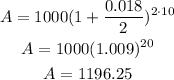
The balance after 10 years will be $1196.25
c) Add both results to determine the final balance after 100 years:
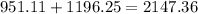
Max's balance after 10 years will be $2147.36
5) Finally, to determine who will win the $10000 after 10 years, you have to compare the results of all previous calculations:
Albert: $2159.07
Marie: $2244.99
Hans: $2188.35.
Max: $2147.36
As you can see Marie made the most after the 10 years, so she will receive the $10,000