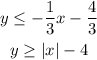Question

Write a system of inequalities whose solution in the shaded region.....................

Answer 1

We have to identify the inequalities whose solution is shown as in the shaded region.

Identifying first inequality:

From the graph, (x1, y1)=(2, -2) and (x2, y2)=(-4, 0) is a point on the straight line.

The equation of the line can be derived using the formula for two point form as,

`\begin{gathered} y-y1=(y2-y1)/(x2-x1)(x-x1) \\ y-(-2)=(0-(-2))/(-4-2)(x-2) \\ y+2=(2)/(-6)(x-2) \\ y+2=(-1)/(3)(x-2) \\ y=(-1)/(3)x+(2)/(3)-2 \\ y=(-1)/(3)x+(2-2\cdot3)/(3) \\ y=(-1)/(3)x+(2-6)/(3) \\ y=(-1)/(3)x-(4)/(3) \end{gathered}`

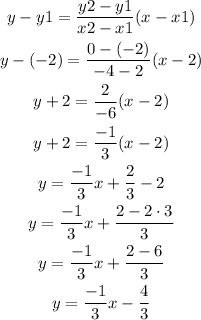
So, the equation of the line govering the inequality is y=-1/3x-4/3.

Since the line is a solid one, the symbol for the inequality is either ≤ or ≥.

Since the region below the line is shaded, the inequality should be of the form y≤.

So, one of the inequality is ,

`y\le-(1)/(3)x-(4)/(3)`

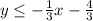
Identifying second inequality:

Now, the v shaped graph governing the inequality is of a modulus function shifted 4 units down.

Hence, the equation for this inequality graph can be written as,

`y=|x|-4`

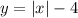
Since the graph is a solid one, the symbol for the inequality is either ≤ or ≥.

Since the region above the graph is shaded, the inequality should be of the form y≥.

So, the inequality expression can be written as,

`y\ge|x|-4`

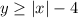
Therefore, the system of inequalities whose solution is in the shaded region is,

`\begin{gathered} y\le-(1)/(3)x-(4)/(3) \\ y\ge|x|-4 \end{gathered}`