Given data:
375, 210, 150, 147, 429, 189, 320, 580, 407, 180
First, rearrange the data from lowest to highest, and we get the data set
147, 150, 180, 189, 210, 320, 375, 407, 429, 580
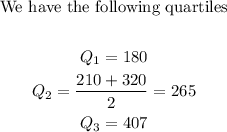
The IQR is determined by the formula
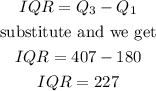
Therefore, the IQR of the data set is 227.