Question

Please help me ASAP!!!!

Answer 1

Let's solve the equation:

`\begin{gathered} \lvert x+2\rvert=0 \\ x+2=\pm0 \\ x=-2\pm0 \\ x=-2 \end{gathered}`

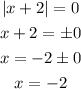
Let's now solve the inequality:

`\begin{gathered} \lvert x+2\rvert\ge0 \\ x+2\ge0\lor x+2\leq0 \\ x\ge-2\lor x\leq-2 \end{gathered}`

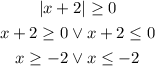
Therefore the solution of the inequality is:

`(-\infty,-2\rbrack\cup\lbrack-2,\infty)`

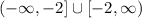
Once we know both solutions we conclude that:

The equation has one solution and the inequality have a range of solutions. Therefore the correct choice is the third option.