SOLUTION:
Case: Binomial Probability
Method:
The formula for the probability is:
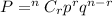
number of rolls, n= 7
required outcomes, r>= 5
prob of obtaining a 5, p= 1/6
prob of not obtaining a 5, q= 5/6
Hence:
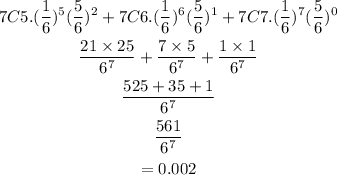
Final answer:
The probability of obtaining at least 5 twos is: 0.002