Question

In the diagram of △KLM below, m∠L=70, m∠M=50, and MK is extended through N.What is the measure of ∠LKN?

Answer 1

Let's begin by listing out the information given to us:

The figure before us is triangle. It is worth noting that the sum of angles in a triangle is 180 degrees

`\begin{gathered} m\angle L=70^(\circ) \\ m\angle M=50^(\circ) \end{gathered}`

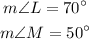
To find the angle at K (m∠LKM), we will subtract the sum of angles L & M from 180 degrees (the sum of angles in a triangle). We have:

`\begin{gathered} m\angle LKM=180-(m\angle L+m\angle M) \\ m\angle LKM=180-(70+50)=180-120=60 \\ m\angle LKM=60^(\circ) \end{gathered}`

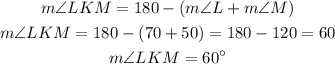
To find the angle at LKN (m∠LKN), we will subtract angle LKM from 180 degrees (the sum of angles on a straight line). We have:

`\begin{gathered} m\angle LKN+m\angle LKM=180^(\circ) \\ m\angle LKM=60^(\circ) \\ m\angle LKN+60=180 \\ m\angle LKN=180-60=120 \\ m\angle LKN=120^(\circ) \end{gathered}`

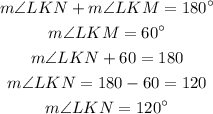
Therefore, m∠LKN is equal to 120 degrees