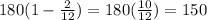Question

find the measure of each interior angle of each regular polygon show all work quadrilateral Pentagon ,dodecagon

Answer 1

We can start with the statement that the sum of all exterior angles of a polygon will add 360 degrees.

For example, for the quadrilateral (square):

Then, each exterior angle must have a value of 360/n.

n is the number of sides.

In the case of the square, n is 4.

For a pentagon, n=5.

The interior angles are supplementary of the exterior angles, so they have a value of:

`180-mExt=180-(360)/(n)=180\cdot(1-(2)/(n))`

For a quadrilateral the measure of the interior angle is 90 degrees:

`180(1-(2)/(4))=180(1-(1)/(2))=180\cdot(1)/(2)=90`

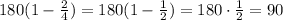
For a pentagon (n=5), the measure of the interior angle is 108 degrees.

`180(1-(2)/(5))=180\cdot(3)/(5)=108`

For a dodecagon (n=12), we have a measure of 150 degrees for the interior angle:

`180(1-(2)/(12))=180((10)/(12))=150`