Question

Two pieces of window glass are separated by a distance, d. If a beam of light of wavelength l=666 nm passes through the first piece of glass. What is the minimum distance, in nm, such that the light intensity transmitted through the right is a maximum?

Answer 1

`\begin{equation*} 333\text{ }nm \end{equation*}`

Step-by-step explanation

Parameters given:

Wavelength of the light, λ = 666 nm = 666 * 10^(-9) m

θ = 90°

n = 1

To find the minimum distance such that the light transmitted through the right is a maximum, we apply the formula:

`\sin\theta=(n\lambda)/(2d)`

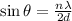
where d = minimum distance.

Therefore, solving for d, we have that the minimum distance is:

`\begin{gathered} \sin90=(1*666*10^(-9))/(2*d) \\ \\ 1=(666*10^(-9))/(2*d) \\ \\ d=(666*10^(-9))/(2) \\ \\ d=333*10^(-9)\text{ }m=333\text{ }nm \end{gathered}`

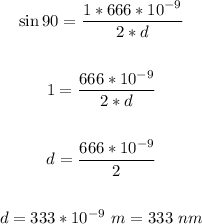
That is the answer.