The sine of theta is given by the y-coordinate of point P:
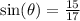
The cosine of theta is given by the x-coordinate of point P, so we have:
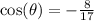
The tangent can be calculated as the sine divided by the cosine:
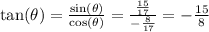
The cosecant is the inverse of the sine:
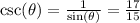
The secant is the inverse of the cosine:
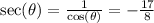
And the cotangent is the inverse of the tangent:
