Question

Newton's law of where is the temperature of the object at timerand is the constant temperature of the surrounding mediumSuppose that the room temperature and the temperature of a cup of tea 160 degrees when it is placed on the tableHow will it take for the tea to to 120 degrees for k = 0.0599437 Round your answer to two decimal places

Answer 1

We know that Newton's law of cooling is:

`T=Ae^(-kt)+C`

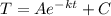
In this case, the initial temperature of the cup is 160° which means that A=160, the temperature of the room is 71° then C=71 and the value of k is 0.0595943 then the function describing the temperature of the cup at any given time is:

`T=160e^(-0.0595943t)+71`

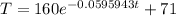
Once we have the function, we can determine the time it takes the cup to have a temperature of 120°, to do this we plug T=120 in the function and solve for t:

`\begin{gathered} 120=160e^(-0.0595943t)+71 \\ 160e^(-0.0595943t)=120-71 \\ 160e^(-0.0595943t)=49 \\ e^(-0.0595943t)=(49)/(160) \\ \ln e^(-0.0595943t)=\ln(49)/(160) \\ -0.0595943t=\ln(49)/(160) \\ t=(1)/(-0.0595943)\ln(49)/(160) \\ t=19.86 \end{gathered}`

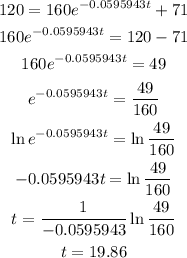
Therefore, the time it takes for the cup to be at 120° is 19.86 minutes