Question

Help solving e 27 log2(4)^3e=864(1/16)

Answer 1

e = 1/3

Step-by-step explanation:

The initial expression is:

`27\log _24^(3e)=864((1)/(16))`

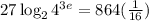
First, let's divide 864 by 16 to get:

`\begin{gathered} 27\log _24^(3e)=(864)/(16) \\ 27\log _24^(3e)=54 \end{gathered}`

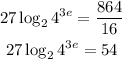
Now, divide both sides by 27

`\begin{gathered} (27\log _24^(3e))/(27)=(54)/(27) \\ \log _24^(3e)=2 \end{gathered}`

Then, by properties of the logarithms, the exponent of the 4 can multiply the expression as:

`3e\log _24=2`

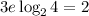
Since log₂4 = 2, we get:

`\begin{gathered} 3e(2)=2 \\ 6e=2 \\ (6e)/(6)=(2)/(6) \\ e=(1)/(3) \end{gathered}`

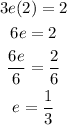
Therefore, the value of e is 1/3