The projectile will land on the desert when h = 0, in other words
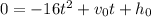
Now, we are told that h_o = 2400ft and v_o = 400ft/s; and putting those in the formula above gives
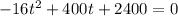
Now this is a quadratic equation and the solution is given by
![\begin{gathered} ax^2+bx+c=0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/uuterq6bz1kwr2mb9jy58c523r5v4v644y.png)
In our case, a = -16, b = 400, and c = 2400; therefore, the quadratic formula above gives
![t=\frac{-400\pm\sqrt[]{400^2-4(-16)(2400)}}{2(-16)}](https://img.qammunity.org/2023/formulas/mathematics/college/phjashn2l083cmlj7yqauyk58lnil8f0f0.png)
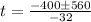
Hence, the two solutions are
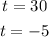
Since negative values of t have no physical significance, the valid answer is t = 30s.
Hence, the third choice in the column is the right answer.