Question

Which one of these is NOT equal to linear velocity?a.v2/r b.displacement/time c.2πfrd.ωr

Answer 1

The linear velocity in terms of the angular velocity is,

`v=\omega r`

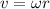
where,

`\omega\text{ is the angular velocity, r is the radius of the circular motion}`

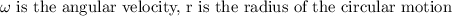
The angular velocity in terms of the linear frequency is,

`\omega=2\pi f`

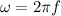
Thus, the linear velocity in terms of linear frequency is,

`v=2\pi fr`

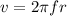
The linear velocity in terms of the displacement and time is,

`v=\frac{\text{displacement}}{\text{time}}`

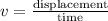
The relation given in the first option is the expression for centripetal acceleration.

`a_c=(v^2)/(r)`

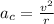
Thus, option a is the correct answer.