Question

Write the equation of the line that is parallel to line 7−4x=7y through the point (2,0).A. y=−4/7x+7/8B. y=8/7x−4/7C. y=−4/7x+8/7D. y=−4/7x−8/7

Answer 1

Step1: Write out the giving equation

`7-4x=7y`

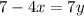
Step2: Write out the equation in form of y=mx+c

`\begin{gathered} 7-4x=7y \\ 7y=-4x+7 \\ \text{ Divide both sides by 7} \\ y=-(4)/(7)x+1 \end{gathered}`

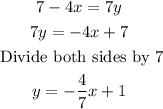
Then the gradient of the equation is the coefficient of x

`\text{ gradient, m=-}(4)/(7)`

Two lines are parallel if their gradient is the same

Hence the second line will have a gradient of

`m_2=-(4)/(7)`

Step4: Apply the slope and one point form to find the gradient of the line parallel to 7-4x=7y

`\begin{gathered} y-y_1=m_2(x-x_1) \\ \text{where the point given is (2,0)} \\ y_1=0,x_1=2 \end{gathered}`

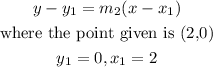
The substitute the parameters into the formula

`\begin{gathered} y-0=-(4)/(7)(x-2) \\ y=-(4)/(7)x+(8)/(7) \end{gathered}`

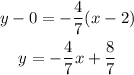
Therefore the equation of the line is y = -4/7x+8/7

The right option is C