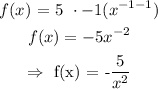ANSWER
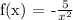
Step-by-step explanation
We want to find the derivative of:
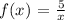
To do that, we have to rewrite the fraction in index form:
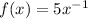
Now, to differentiate the function with respect to x, we will mutliply the coefficient of x (5) with the power of x (-1) and then subtract 1 from its power.
That is: