Question

Family took a road trip. After a while they stopped for gas. Then they traveled 58 3/4 miles and stopped for lunch. After lunch they travelled tripled their distance before stopping for the night. Their total distance was 381 miles. How many miles did they travel before their first stop for gas?

Answer 1

We are given the following information

After a while they stopped for gas.

Then they traveled 58 3/4 miles and stopped for lunch.

After lunch, they traveled tripled their distance before stopping for the night.

Their total distance was 381 miles.

Let x be the distance they travel before their first stop for gas.

So, the equation must be 3 times the distance x plus 58 3/4 miles and it must be equal to the total distance they traveled.

`3(x+58(3)/(4))=381`

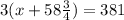
Now, let us solve the above equation for x.

Divide both sides of the equation by 3.

`\begin{gathered} (3(x+58(2)/(4)))/(3)=(381)/(3) \\ x+58(3)/(4)=127 \end{gathered}`

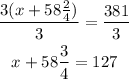
Now, subtract 58 3/4 from both sides of the equation.

`\begin{gathered} x+58(3)/(4)-58(3)/(4)=127-58(3)/(4) \\ x=68(1)/(4)\;miles \end{gathered}`

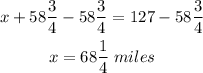
Therefore, the distance they travel before their first stop for gas is 68 1/4 miles.