Question

Locate any points of inflection. Enter your answer as (×, y)-pairs.

Answer 1

Step 1:

Concept

An inflection point is a point on the graph of a function at which the concavity changes. Points of inflection can occur where the second derivative is zero. In other words, solve f '' = 0 to find the potential inflection points. Even if f ''(c) = 0, you can't conclude that there is an inflection at x = c.

Step 2:

Find the first derivative of the function.

`\begin{gathered} f(x)=5x^3-30x^2\text{ - 7x - 2} \\ f^(\prime)(x)=15x^2\text{ - 60x - 7} \end{gathered}`

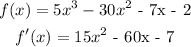
Step 3:

Find the second derivative

`\begin{gathered} f^(\prime)(x)=15x^2\text{ - 60x - 7} \\ f^(\doubleprime)(x)\text{ = 30x - 60} \end{gathered}`

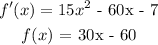
Step 4:

Next, set the second derivative equal to zero and solve. Because f '' is a polynomial, we have to factor it to find its roots.

`\begin{gathered} 30x\text{ - 60 = 0} \\ 30x\text{ = 60} \\ \text{x = }(60)/(30) \\ \text{x = 2} \end{gathered}`

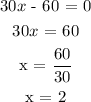
The solution is x = 2

Final answer

`\begin{gathered} f(x)=5x^3-30x^2-7x\text{ - 2} \\ =5(2)^3-30(2)^2-7(2)\text{ - 2} \\ \text{= 40 - 120 - 14 - 2} \\ =\text{ }-96 \end{gathered}`

Inflection point = (2 , -96)