Question

_____cosb = [sin (a + b) + sin(a - b)]OA. cosaOB. cosbOC. sinaOD. sinb

Answer 1

We need to complete the following identity:

`\text{ \_\_\_\_}*\cos b=(1)/(2)[\sin(a+b)+\sin(a-b)]`

For solving this problem, we need to check some known trigonometric identities, in this case we can use the following product identity:

`\sin\alpha\cos\beta=(\sin(\alpha+\beta)+\sin(\alpha-\beta))/(2)`

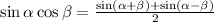
If we replace alpha by a and beta by b, we obtain:

`\begin{gathered} \sin a*\cos b=(\sin(a+b)+\sin(a-b))/(2) \\ \\ \text{ And this is equal to:} \\ \sin a\cos b=(1)/(2)[\sin(a+b)+\sin(a-b)] \end{gathered}`

The answer is C. sin a.