Question

Hi, can you help me answer this question, please, thank you:)

Answer 1

Notice that the total probability is distributed in 8 minutes. Furthermore, the total probability has to be equal to 1, then:

`\begin{gathered} h\cdot8=1 \\ \Rightarrow h=(1)/(8)=0.125 \end{gathered}`

Where h is the height of the distribution. The first answer is 0.125.

b) Notice that 16-13=3 min. Therefore, the probability we are looking for is:

Thus, the probability that will we wait more than 15 minutes is:

`P(X>15)=1-0.75=0.25`

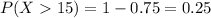
The third answer is 0.25

d) The probability that one will wait at most 15 minutes was found in the previous step:

`P(X\le15)=(15-9)/(8)=(6)/(8)=0.75`

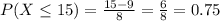
The fourth answer is 0.75