Question

A motel rents double rooms at $32 per day and single rooms at $26 per day. If 23 rooms were rented one day for a total of $688, how many rooms of each kind were rented? *

Answer 1

To solve the exercise you can propose the following system of linear equations:

`\begin{gathered} x+y=23\Rightarrow\text{ Equation 1} \\ 32x+26y=688\text{ }\Rightarrow\text{ Equation 2} \\ \text{ Where} \\ x\text{ is the number of double rooms and} \\ y\text{ is the number of single rooms} \end{gathered}`

To solve the system of linear equations you can use the method of reduction or elimination. To do this first multiply Equation 1 by -32 and add both equations, then solve for the variable y:

`\begin{gathered} (x+y)\cdot-32=23\cdot-32 \\ -32x-32y=-736 \\ \text{ Now add both equations} \\ -32x-32y=-736 \\ 32x+26y=688\text{ +} \\ ------------- \\ 0x-6y=-48 \\ -6y=-48 \\ \text{ Divide by -6 from both sides of the equation} \\ (-6y)/(-6)=(-48)/(-6) \\ y=8 \end{gathered}`

Finally, replace the value of the variable y into any of the initial equations and solve for the variable x. For example, replace the value of the variable y in Equation 1:

`\begin{gathered} x+y=23 \\ x+8=23 \\ \text{ Subtract 8 from both sides of the equation} \\ x+8-8=23-8 \\ x=15 \end{gathered}`

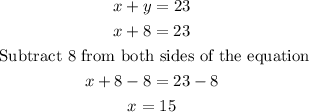
Therefore, 15 double rooms and 8 single rooms were rented.