Question

I have been trying to do this problem for a very long time and I have no idea what I am doing wrong please help me. i just guessed the right answer but I need to understand.

Answer 1

We have to solve:

`\begin{gathered} (2)/(3z)-((5)/(6z^2)-(z+3)/(z)) \\ (2)/(3z)-((5)/(6z^2)-(6z)/(6z)\cdot(z+3)/(z)) \\ (2)/(3z)-((5)/(6z^2)-(6z(z+3))/(6z^2)) \\ (2)/(3z)-((5-6z(z+3))/(6z^2)) \\ (2)/(3z)-((5-6z^2-18z)/(6z^2)) \\ (2)/(3z)\cdot(2z)/(2z)-((5-6z^2-18z)/(6z^2)) \\ (4z)/(6z^2)-((5-6z^2-18z)/(6z^2)) \\ (4z-5+6z^2+18z)/(6z^2) \\ (6z^2+22z-5)/(6z^2) \end{gathered}`

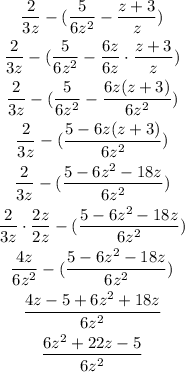
For the first factor, when we have to substract the fractions inside the parenthesis, we have to find the common factors between 6z^2 and z. In this case, z is part of 6z^2, so we have to multiply z by 6z^2/z=6z.

If we multiply the fraction by 6z/6z we don't change the result and get the same denominator in order to do teh substraction.

In the 6th step, we have to convert the denominator 3z into 6z^2. We can find the factor by dividing 6z^2 by 3z:

`(6z^2)/(3z)=(6)/(3)\cdot(z^2)/(z)=2z`

With this factor, 2z, we can convert the denominator from 3z to 6z^2 and perform the operation.

Answer: (6z^2+22z-5)/6z^2