Question

Solve the system by any method you choose: .No solution exists.There are an infinite number of solutions.(0, –1)(1, 0)

Answer 1

We are given the following system of equations

`\begin{gathered} -(1)/(2)x-4y=4 \\ 2x+16y=2 \end{gathered}`

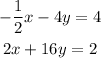
Let us solve the above system of equations using the elimination method.

Suppose we want to cancel the x terms, then we have to multiply eq.1 by 4.

`4\cdot(-(1)/(2)x-4y=4)\Rightarrow-2x-16y=16`

Now, add the two equations

As you can see, after adding the equations we get 0 = 18 which cannot be true.

This means that no solution exists for this system of linear equations.