Question

3/5t + 7 = -8 I need help solving this

Answer 1

The expression we have is:

`(3)/(5)t+7=-8`

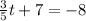
Step 1. Substract 7 from both sides of the equation:

`\begin{gathered} (3)/(5)t+7-7=-8-7 \\ (3)/(5)t=-15 \end{gathered}`

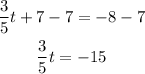
Step 2. Multiply both sides by 5/3 to eliminat the 3/5 on the left:

`(5)/(3)*(3)/(5)t=(5)/(3)*(-15)`

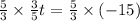
On the left we are left only with t:

`t=(5)/(3)*(-15)`

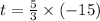
Step 3. Solve the multiplication on the right side:

`\begin{gathered} t=-(5*15)/(3) \\ t=-(75)/(3) \end{gathered}`

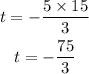
Step 4. Solve the division to find the final value of t:

`t=-25`